観光都市

概要

生活の中にあるさまざまな問題は、学習13の彩色問題で使われたようなネットワークや「グラフ」の形に抽象化できます。ネットワークは、実用的なアルゴリズムを考える多くの機会を提供します。この学習で、私たちは「すべての交差点(「ノード」と呼びます)が、印を付けたノードから1つ以内の距離にある」ようにいくつか のノードに印を付けることを考えます。条件を満たしながら、印を付ける交差点をいかに少なくできるかがここでの問題です。これはやってみると、驚くほど難しい問題であることがわかります。

教科学習との関連

• [数学]位置と方位

技能

• 地図
• 関係
• パズルを解く
• 繰り返してゴールを探す

年齢

• 7 歳以上

教材

• 子どもごとに必要なもの
  • ワークシートのコピー　PDF
  • 2つの異なる色のおはじき、または、それに代わるもの

• 教師に必要なもの
  • ワークシート「アイスクリームワゴンの解答」　PDF
  • または、それを描くための黒板

• ワークシート
  • 解説　PDF

• 授業用補足資料　PDF

支配集合

はじめに

ワークシート「アイスクリームワゴン」に示しているのは、観光都市の地図です。線は通り、点は交差点を表 しています。その都市はとても暑い国にあり、夏の間はアイスクリームワゴンが交差点に止まって、観光客にアイスクリームを売ります。私たちは、誰もが通りの端まで、すなわち高々1ブロック歩けばアイスクリームを買えるようにワゴンを置きたいと考えます。(人々が通りの途中に居るのではなく交差点に居て、少なくとも1ブロック歩けばアイスクリームを買えるようにしなければいけないと考えた方がわかりやすいかも知れません。) この問題は、ワゴンが何台必要で、それをどの交差点に置けばよいかというものになります。

議論

1. 子供たちを少人数のグループに分け、それぞれのグループに観光地の地図といくつかのおはじきを渡し、物語の説明をします。
2. 子どもたちに、1つのアイスクリームワゴンの場所を示すために交差点におはじきを置くことと、1ブロック離れた交差点に違う色のおはじきを置くことを説明します。おはじきが置かれた交差点(またはその交差点につながる通り)に居る人々は、このワゴンからアイスクリームを買います。
3. 子どもたちに、違う位置にワゴンを置かせてみましょう。子どもたちがすべての場所からアイスクリームを買いに行けるワゴンの配置を見つけられるようになったら、ワゴンは高価なので、できるだけ少ない台数にしたいことを思い出させます。すべての交差点に配置するだけのワゴンがあれば、すべての場所から 買いに行ける条件を満たすことは明らかです。それをどれだけ少なくできるのかが、おもしろい問題なのです。
4. この観光地に必要なワゴンの数は最小6台で、このに示したものが解の1つです。しかし、この解を見つけることはとても難しいのです。しばらく考えさせたら、6台のワゴンで十分なことを告げ、その置き方を見つけることにチャレンジさせます。これでもまだ難しい問題なので、多くのグループは結局諦めてし まうでしょう。8台や9台のワゴンを使っても、解を見つけるのは難しいかも知れません。
   
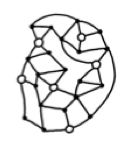
5. この観光地の地図はワークシート「アイスクリームワゴンの解答」の下の図に描かれた、明らかにそれぞ れにワゴンが1台だけ必要な6つの地図の断片から作り始められました。そして、解をわかりにくくする ためのたくさんの通りをつないでいったのです。大切なことは、解となるワゴンを置く交差点(白丸)同 士はつなげず、それ以外の交差点(黒丸)同士のみをつなげることです。OHPか黒板でこのことをクラ スの子どもたちに説明します。
6. この戦略を使って、子どもたちにオリジナルの難しい地図を作らせます。子どもたちは、それを友達や両 親に解かせてみたいと思い、そして、自分たちは解けるけれど他の人には解けないパズルを作り出すこと に夢中になることでしょう。これらはいわゆる「一方向関数」の例で、最初に作った本人でなければ解く ことがとても難しいパズルを簡単に作れるものなのです。一方向関数は、暗号で重要な役割を演じます。(学習17と18を参照)