貧乏な地図職人
貧乏な地図職人
概要
多くの最適化問題には、あるできごとが同時に起きてはいけないとか、集合のある要素同士が隣り合ってはいけないといった状況が含まれます。たとえば、授業の時間割を作ったり、会議の予定をたてる人は、関係するすべての人が出席することができるよう制約を満たさなくてはならないという問題に直面します。このような困難さを持つ問題は、隣り合う国が区別できるよう違う色となるように国ごとの色を選ぶという「地図彩色問題」として表すことができます。ここではその問題について扱っていきます。
教科学習との関連
- [数]10以外を基数とした数を学ぶ。基数を2とした数を表現する。
- [代数]連続したパターンの続きを求め、そのパターンの規則を説明する。2のべき乗のパターンと関係を理解する。
技能
- 問題解決
- 論理的推論
- アルゴリズム的な手順と複雑さ
- 本質を見抜くコミュニケーション
年齢
- 7 歳以上
教材
黒板など書き込めるもの
- 子どもごとに必要なもの
- 1 枚以上のワークシートのコピー
- 色のついたおはじき
- 四色のクレヨン(または色鉛筆、サインペンなど)
- ワークシート
- 授業用補足資料
 PDF
PDF
グラフ彩色
はじめに
この学習は、「子どもたちが、地図上の国に色を塗る地図職人(または地図作成者)の仕事を手伝うよう頼まれている。」というストーリーで進めていきます。隣り合う国同士の色が異なるならば、どの国にどの色を塗ってもかまいません。
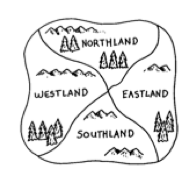
たとえば、この地図には4つの国があります。「北の国」を赤で塗ると、「西の国」と「東の国」は赤にできません。北の国の境界がわからなくなるからです。西の国を緑に塗れば、東の国は境界を西の国と共有しないので 緑で塗ることができます。(2つの国が1個の点だけで接するときは、境界を共有していることとはしないため、 同じ色で塗ることができます。)そして、「南の国」は赤で塗ることができるので、この地図はたった 2 色で塗ることができるます。
ここでは、地図職人は貧乏で多くのクレヨンを使うお金がないため、できるだけ少ない色で地図を塗りたいと
いうストーリーにしています。
議論
色塗りの手順を黒板でしめしながら、子どもたちが取り組む問題を説明します。
ワークシート1のコピーを配布します。この地図は2色だけで正しく塗ることができます。色数を2色だけに制限することで問題がとても難しくなるように思えるかもしれませんが、それぞれの国に塗ることができる色の選択肢がほとんどないため、より多くの色を必要とする地図と比べて、作業はとても簡単になります。
子どもたちに、2色だけを使って地図を塗らせてみてください。この作業の中で、子どもたちは「いったん1つの国に色を塗ったら、隣り合う国はすべてもう一方の色で塗らなければいけない」という「あたりまえ」の規則を発見するでしょう。全ての国に色が塗られるまで、この規則は繰り返し適用されます。もし、教えられるのではなく、子どもたちが自らこの規則を発見できるならば、子どもたちがより本質を見抜く力(洞察力)を得たこととなり、最高の学習となります。
子どもたちが各々の演習を終えたら、続くワークシートを手渡していきます。
子どもたちは、試行錯誤しやすいように、国を塗っていく代わりに、色のついたおはじきのような物を置いて行く方が良いことに気づくかもしれません。
高学年の子どもには、どのようにして最低限の色の数を見つけたか説明させてみましょう。例えば、ワーク シート3の地図は最低 3 色必要です。それは、境界を互いに共有している3つの国のグループがあるからです。(一番大きな3つの国がそれです。)
もし全てのワークシートを早く終わらせた子どもがいたら、 5色の異なる色が必要な地図を考えさせてみます。どんな地図も4色で塗り分けられることは証明されているので、彼らをしばらくこの作業にひきつけておくことができるでしょう! 私たちの経験では、すぐに子どもたちは自分たちでは5色だと思う地図を見つけます。 しかし、もちろんいつも、それらの地図を4色で塗る解を見つけることができるのです。