氷上の道

概要

取るに足らないように見える問題の中身の小さな違いが、解決の難しさを大きく変えることがあります。 この章では、学習9のマッディ市のような、ネットワーク上の最短の経路を見つける問題を扱います。 異なることは、経路長を短くできるのであれば、ネットワークに新しい点を加えることができるということです。

その結果は、マッディ市よりはるかに難しい問題となり、アルゴリズム的には 13 章や 14 章と同等のものになります。

技能

• 空間的な視覚化
• 幾何学的な推論
• アルゴリズム的な手順と複雑さ

年齢

• 7 歳以上

必要な能力

• 紐の長さを測ること、それらの長さを合計できること
• 子どもたちは、紐を釘に結べる必要があります

時間

20分以上
子どもたちが外の芝生で活動する場合は、天気が悪くないことが必要です

教材

• 子どもごとに必要なもの
  • 子どものグループごとに、5,6 本の杭を地面に挿す必要がある。(テントの留め具がよいが、洋服のハンガーを分解して曲げたものでも構わない)
  • 紐かゴムひもを数メートル、定規か巻尺、記録するためのペンと紙。

• ワークシート
  • 応用と解説　PDF

• 授業用補足資料　PDF

活動

はじめに

前章では舞台は暑い場所だったが、この章ではちょうど逆となります。

氷で覆われたカナダ北部の冬、いくつかの掘削地点にいる作業員が互いに行き来できるように、除雪車がそれぞれの掘削地点を結ぶ道を凍った大きな湖の上に作ります。 外は寒いので、道を作る作業は最低限にしたいと思います。そこで道をどこに作ればよいかを考えてください。

道を作るに当たっての制限は何もありません。道は凍った湖の雪の上の、どこにでも作れます。また、全体は平坦です。

道は曲がっていると不必要に長くなってしまうため、明らかに直線で延していくべきです。

しかし、それはすべての掘削地点をそれぞれ直線で結べばよいというほど単純なことでありません。なぜなら極寒の荒野に交点を加えることで、ときに合計の経路の長さを減らすことにもなりうるからです。ここで重要なことは道全体の長さであって、ひとつの場所から別の場所への移動時間ではありません。

図の1(a) は 3 箇所の掘削地点を示しています。

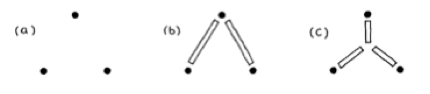
ある掘削地点と他の2つの掘削地点とをつなぐ方法として、まず考えられるのは図 15-1(b) のような道をつく ることでしょう。

もう一つの考えられる方法としては、図 15-1(c) の様に三角形の中心近くに交差点をつくり、それを三つの掘 削地点と結び付けることがあります。

もし、すべての道の長さを合計して他の物より短くなっていれば、これが実際により良い解となります。

この追加された交差点は、シュタイナーの点と呼ばれています。これは、新たな点を追加することで距離の合 計を減らすことができることを最初に指摘したスイスの数学者ヤコブ・シュタイナー(1796-1863)にちなんで 付けられたものです。
シュタイナーの点は新しい架空の掘削地点とみなすこともできます。

1. 子供たちが取り組む問題について説明を行います。
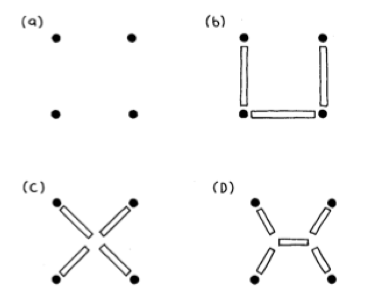
   上の図の例を使い、3 地点を結ぶ場合には、新しい地点を加えることで道路工事の総量を減らすことができ、よりよい解を導くことが出来る場合があることを示します。
2. 子供たちには、下の図2a の様に正方形に配置された 4 個の点を使います。 外に出て、それぞれのグループで一辺が 1 メートルの正方形になるように 4 個の杭を芝の上に挿し込ませます。
   
3. 子どもたちに杭を紐やゴムひもで結ばせて、最短となる長さの合計を測り記録させます。
   この段階ではまだシュタイナー点を使ってはいけません。(この場合の最短となるのは、図 15-2(b) で示される正方形の三辺を結ぶもので、長さは 3 メートルとなります。)
4. ここで、子供たちにシュタイナー点を一つ使って、全体の長さがより短くできるかどうかを試させます。(この場合は、シュタイナー点を図の2(c) の様に四角形の中心に持ってくるのが最短となり、2√2 =約 2.83 メートルとなります。)
   次に、シュタイナー点を 2 個使うことで、さらに短くすることができるかもしれないということを提案します。 (実際、図の2(d) のように 120 度の角度で線を引くことで、2 個の点を置くことができます。この場合の長さの合計は 1+ √ 3 = 2.73 メートルとなります。)
5. 子どもたちはシュタイナー点を 3 個にして、さらに改良できるでしょうか?
   (この場合、シュタイナー点は 2 個の場合が最短となり、3 個以上使っても改善されません。) + 子どもたちと、どうしてこれらの問題が難しいかを議論します。
   (理由は、まず、シュタイナー点をどこに置けばよいかがわからないということ。更に、置くことのできる可能性が無数にあることです。)