子ども暗号
子ども暗号
概要
暗号化は情報セキュリティの要です。
そして、現代の暗号化の要は、送信者が公開された情報だけを使ってメッセージに錠をかけて、意図された受信者だけが(もちろん秘密のうちに)錠を開けられるようになっていることです。
ちょうど、ひとりひとりが南京錠を買って、自分の名前を書いて、みんなが共通のテーブルに置いてほかの人に使ってもらうようなものです。
もちろん、鍵はひとりひとりが持っておきます。南京錠は、単にかちっと押し込めば閉じるようなものとします。
私があなたに安全にメッセージを送るときには、私はメッセージを箱に入れて、あなたの南京錠を取って、箱に錠をかけてあなたに送ります。
そうすると、たとえ箱がほかの人の手に渡っても、あなた以外のだれも錠を開けられません。
この仕組みを使えば、暗号方式を決めるために事前に打ち合わせをする必要がありません。
この学習では、この仕組みを数値を使って実現する方法を学びます。 数値の世界では、南京錠をテーブルから取って使うかわりに、錠の現物をテーブルに置いたまま、複製して、その複製物を使います。
本物の南京錠を複製しようと思ったら、錠を分解するほかありません。 そんなことをしたら、どうしても、錠の仕掛けがわかってしまいます。 でも、数値の世界でなら、鍵を発見されることなく、錠を複製してもらうことができるのです! そんなこと、できるわけないと思う? 続きを読んでごらんなさい。
技能
- パズルを解く
- 暗号
年齢
- 12歳以上
必要な能力
この学習はこの本の中で最も高度な技量を必要とする学習です。
やりがいはあるものの、最後まできちんとやり遂げて成功させるためには,注意深い作業と集中力の持続が必要です。
子どもたちは、この学習に先立って、学習 14:ツーリストタウンの一方向関数の例を学習している必要があります。また、この分野のほかの学習(学習16「秘密を共有する」学習 17「ペルーのコイン投げ」)をすでに学習していると,この学習に役立ちます。
この学習では、学習1「点を数える」、学習5「20の扉」で扱った知識も使います。
時間
およそ30分
教材
子どもたちを 4 人ぐらいのグループに分け、さらに、それぞれのグループの中でふたつの小グループを作ります。
- 子どものグループごとに必要なもの
- ブラックラインマスターのコピー 2枚
 PDF
PDF
- ブラックラインマスターのコピー 2枚
- ほかに必要なもの
- ワークシートのコピー
 PDF
PDF - 図に注釈を書き込む手段
- ワークシートのコピー
- ワークシート
- 解説
 PDF
PDF
- 解説
- 授業用補足資料
 PDF
PDF
活動
エイミーはビルに秘密のメッセージを送ろうとしています。
普通は、秘密のメッセージといえば、文とかパラグラフだと思うでしょう。でも、この実習では、エイミーは 1 個の文字だけを送ります。実際には、1 文字を表現する 1 個の数を送ります。
これは単純すぎるメッセージと思うかもしれません。でも、こう思ってください。彼女はこういう「メッセージ」を続けてたくさん送って、文を完成させることができます。そして、実際はそういう作業はコンピュータがやってくれます。
場合によっては、小さなメッセージでさえも重要な意味を持つことだってあります。なにしろ、歴史に残る最 も記念すべきメッセージのひとつである、ポール・リビアが伝えたメッセージは、とりうる値がたった 2 個だったのですから。
私たちは、ビルの公開された錠を使ってエイミーの数を暗号化されたメッセージに埋め込んで、誰かがメッ セージを横取りしたとしても解読できないようにする方法を学びます。
ビルだけが解読できます。彼だけが錠を開ける鍵を持っているのですから。 メッセージに錠をかけるために地図を使います。
宝島の地図ではありませんよ。あれは X 印で宝のありかを示しています。そうではなくて、149 ページにあるツーリストタウンの地図のようなものです。線は道路を表し、点は交差点を表します。 地図にはそれぞれ、公開用(錠)と秘密用(鍵)があります。
194 ページに載っているのはビルの公開用の地図です。 これは秘密ではありません。ビルは、この地図をテーブルに(あるいはウェブページに)置いて、みんなに見てもらいます。あるいは、彼にメッセージを送るかもしれない人みんなに地図を手渡しても同じことです。
エイミーは地図の写しを持っています。同じように、ほかの誰もが持っています。
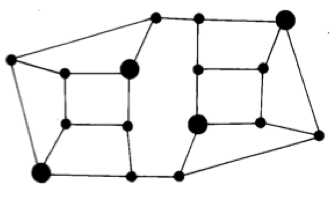
上の図はビルの秘密用の地図です。
これは彼の公開用の地図と同じですが、いくつかの特別な交差点を大きい点で目立たせているところが違います。
彼はこちらの地図を秘密にしておきます。
この学習は、少なくとも最初は、学級全体でするのが最適です。たくさんの作業をしなければならないからです。
作業は、難しくはありませんが、正確にしなければなりません。誤りがあるとたくさんの問題が発生するからです。
重要なのは、子どもたちが、そもそもこんな「できそうにない(と思うでしょ?)」暗号化が実は実現可能であ ることが、驚くべきことだとわかっていることです。そういう動機付けがあってこそ、子どもたちは、頑張って 作業して、どうしてそんな暗号化ができるのかをわかろうとするのです。
私たちが気づいたことですが、学校の生徒は、「この仕組みを使って授業中に秘密のメモを受け渡すことがで きる、そうすると、たとえ教師がメモの暗号化のしかたを知っていようとも、教師は中身を読み取れない」と気づくと、俄然やる気になります。
- ビルの公開用の地図を OHP で映し出します。 エイミーが送ろうとする数を決めてください。 次に、地図の各々の交差点にランダムな数を割り当てて、それらのランダムな数の合計がエイミーが送りたい数になるようにしてください。
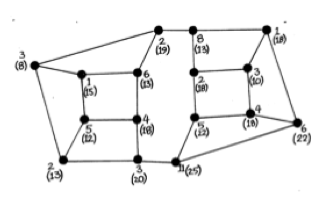
上図は、そういう数の割り当ての例です。それぞれの交差点のそばに書いてある、上側の(括弧がついていない)数がそうです。
ここでは、エイミーは送る数として 66 を選びました。だから、括弧がついていない数の合計が 66 になっています。
必要なら、合計を狙い通りの値にするために、負の数を使ってもかまいません。 - さて、エイミーはビルに送るべきものを計算しなければなりません。 たった今決めた数を書き込んだ地図を送ったのでは意味がありません。ほかの人が手に入れたら、だれでも、すべての数を合計してメッセージを読み取れるからです。 そのかわり、次のようにします。ひとつの交差点を選んで、その交差点と、3 つあるとなりの交差点(つまり全部で 4 つの交差点)に注目して、それらの交差点に書いてある数を合計します。 そうして求めた合計を、選んだ交差点のところに、括弧を付けて書くか、または、違う色のペンで書きます。 たとえば、図 18。2 の最も右の交差点は、ほかの 3 つの交差点とつながっていて、3 つの交差点には 1、 4、 11 と書かれていて、自分自身には 6 と書かれています。
すると合計は 22 です。
この作業を、地図のほかのすべての交差点について繰り返します。
そうすると、図 18。2 の括弧のついた数が求められます。 エイミーは、括弧がついた数だけをビルの地図に書き込んで、ビルに送ります。 もとの数と計算式を消して、エイミーが送るべき数だけを残します。あるいは、送るべき数だけを新しい地図に清書してもよいでしょう。
子どものうち一人でも、もとのメッセージが何だったかをこの地図から知る方法を見出せるかどうか、観察してください。たぶん、子どもたちには無理でしょう。
ビルの秘密鍵を持っている人だけは、メッセージを解読して、エイミーがもともと送りたかったメッセージを知ることができます。
暗号化されたメッセージの書かれた地図を見て、ビルの秘密用の地図で特別な大きい点のところに印をつけます。 メッセージを解読するには、印をつけた秘密の交差点だけに注目して、それらの横に書いてある数を合計します。
この例では、それらの交差点には 13、 13、 22、 18 と書いてあります。それらの合計は 66 で、これはエイミーのもともとのメッセージです。 - どうしてうまくいくのでしょう?
それは、使った地図が特別な地図だからです。
印のついた交差点をひとつ選んで、そこから道路 1 本だけ離れた交差点すべてを線で囲ってみましょう。印のついた交差点ひとつひとつについて、その手続きをします。
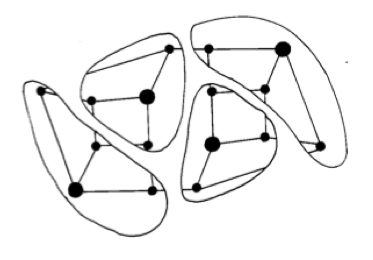
そうすると、図に示されているように、地図は重なりのない断片に分けられます。 これらの断片を、地図に境界線を書き込むことで、子どもたちに示してください。 それぞれの区画にある交差点の集まりは、まさに、印のついた交差点の横に書いて送信する数を計算するために、合計を求めた交差点の集まりと同じです。だから、それらの交差点に書かれて送信された 4 つの数の合計 は、もとの地図に書かれたもとの数すべての合計になります。それはつまり、送りたかったもとのメッセージです!
ふうっ!
1 個の文字を送るだけで、たいへんな重労働ですね。
実際、1 個の文字を送るのは大仕事なのです。暗号化というのはたやすい仕事ではないのです。 でも、成し遂げたことを振り返ってみましょう。公開された鍵を使って完全な秘匿を実現したのです。参加者の間で事前の打ち合わせを一切することなく、あなたの鍵を掲示板に貼り出して公開しておけば、誰でもあなたに秘密のメッセージを送ることができて、しかも、そのメッセージは秘密の鍵がない限りだれも解読できないのです。
そして、現実世界では、ソフトウェアパッケージを入手すれば、必要な計算はすべてやってくれます。重労働をする必要があるのはコンピュータだけです。 たぶん、あなたのクラスは、「公開鍵暗号系の例を手作業で実際にやってのけた自分たちは 『選ばれた数少ない人々』の仲間入りだ」と知れば喜ぶでしょう。現役のコンピュータサイエンティストは、公開鍵暗号系を 手作業で学習するなんてほとんど不可能だと思っていて、そんなことをやってのけた人がいるとは思わないでしょう!
ところで、盗聴された場合は大丈夫なの?
ビルの地図は、観光都市の学習(学習 14)で使ったものと同じで、印のついた交差点は、どの交差点 にいる人も 1 ブロックを超えて歩くことなくアイスクリームを買えるような、最も少ない台数のアイスクリーム 販売車の配置のしかたです。
観光都市で学んだとおり、ビルがそのような地図を作るのは簡単です。
図に示した断片から作 り始めればよいのです。そして、ほかのだれかが、総当たり法以外の方法で、最も少ない台数でのアイスクリー ム販売車の配置のしかたを見つけるのは、ものすごく困難です。
総当たり法は、1 台の車でのあらゆる可能な配置を試す、2 台でのあらゆる可能な配置を試す、というように、 解に行き当たるまで試し続ける方法です。
一般の地図に対して、もっとよい方法があるのかどうか、誰にもわかっていません。たくさんの人々が、よい方法を見つけようと試みたのは間違いないのに!
ビルが十分に複雑な地図、たとえば、交差点が 50 個や 100 個ある地図を使ったら、だれも暗号を破ることは できないように思えます。非常に賢い数学者たちでさえ、これに懸命に試みて失敗したのです。
(でも、実はこれには但し書きが必要です。後の「これって、どういうこと?」を読んでください) クラス全体でひとつの例題をやり終えたら、次に、子どもたちを 4 人ぐらいのグループに分けてください。 各グループの各ペアに、193 ページの原稿の公開用地図を渡します。
それぞれのペアは、「メッセージ」(整数なら何でもよい)を選んで、公開鍵を使ってコード化して、得られた地図を他のグループに渡します。 他のグループは解読を試みるでしょう。でも、秘密用の地図を渡される(あるいは、自分たちで作り出す!)
前に解読に成功することはまずありません。
それから、秘密用の地図を渡して、子どもたちが正しく解読できることを確かめます。
ここまでくれば、各ペアが自分たち自身で地図を作って、秘密用の地図を隠しておいて公開用の地図を(グループ内の)もう一方のペアに手渡すことができます。あるいは、教室の掲示板に貼り出して「公開」してもかまいません。
地図を作る原理はツーリストタウンの学習で説明した方法と同じで、解を隠すために余分な道を付け加えてもかまいません。
ただ、「特別な」点につながる道を余分に付け加えないように気をつけてください。
それをしてしまうと、ある交差点からは 2 台のアイスクリーム販売車に一跳びでたどり着けるようになります。そうなると、ツーリストタウンの状況では問題ないのですが、暗号化をするときには混乱を招きます。
なぜかというと、特別な点を使っても、もはや地図は上の図のように重なりのない断片には分割されなく なってしまうからです。重なりのない断片に分割されることは、この仕掛けがうまくいくためにどうしても必要です。