ErrorControlCoding
9. 誤り制御符号化
9.1. 概要
パリティ手品(上のビデオ)では、手品師は後ろを向いている間に数十枚のカードから裏返されたカードを当てることができます。この手品では、データから誤っている部分を検出して訂正する技術で使われているコンピュータ科学の原理を使っています。詳しくは次の節で説明します。
同じ現象はコンピュータの記憶装置の中で起きています。あなた(やコンピュータ)が目を離した隙に、僅かな原因でデータの一部が壊れてしまうことがあります。壊れたデータを使いたい人はいないでしょうから、それを検知して手品師のように正しい状態に戻してくれることは理想です。
この章ではさまざまな形式のデータ(ハードディスク、CD、フロッピーディスク、携帯電話などで使われているSSD)でデータ誤りから守るための技術を扱います。データはメモリとハードディスクの間や、CPUの内部、ネットワークを介したサーバーとの通信をはじめ、商品に印刷されたバーコードやクレジットカードの番号を含みます。
もしCDの傷やUSBメモリの回路の不具合でデータが変化してしまったことに気づかなければ、正しくないデータはそのまま使われてしまうことになるでしょう。銀行のシステムが何の対処もされていなければ、宇宙線によってメモリ中のたった1ビットの値が変わってしまうことによって口座の残高が変わってしまうかもしれないのです!お店でポテトチップスの袋のバーコードが正しく読まれなければ、シャンプーの値段になってしまうかもしれません。ノートPCからデータが正しく送られなければ、MP3プレーヤーは音楽を正しく再生できないかもしれません。誤り制御符号がこれらを防いでくれていることで、私たちはこれらの問題を心配せずに生活できているのです。
データが変化してしまう要因はいくつか存在します。ネットワークには配線や電気信号や電波の干渉などによるノイズが存在します。ディスクに刻まれたビット信号はとても微細なため、表面の小さな傷もデータの不具合につながります。CDやDVDの表面はむき出しになっているため、保管時の熱や湿気、取り扱い時の傷やホコリで損傷しやすいのです。データの誤りは数字を入力するときにも発生します。書類に口座番号を記入したり、船に積み込んだコンテナの数を記入するときなどです。商品のバーコードはかすれて線が消えたり、逆に黒いゴミが付いたりしますし、読むときに商品が曲がっていたり、スキャナを速く動かしたりすぎたりする可能性があります。記憶装置の中でデータが変化してしまうことをビット崩壊と呼びます。WikiPediaのビット崩壊(bit rot)の項目にはデータが変化してしまう要因が多数紹介されています。
データが変化してしまうことでコンピュータの動作が信頼できなくなってしまう状況を望む人は誰もいないでしょう。どうしたらこの問題を防げるのでしょうか?
誤り制御符号はこれらの誤りが起きたことを検出できますし、可能な場合には元のデータに復元することが可能です。
誤り制御の仕組みによっては、この章のはじめで紹介したパリティのように、壊れたデータから元のデータを復元できます。手品師はどのカードが裏返されたかを当てることができて、元のカードがどの色だったかを復元することができるのです。
他の誤り制御の例として、海外のサーバーから手元のコンピュータに送られてくるデータを考えてみましょう。データはパケットと呼ばれる小さな塊に分割されて送られます。パケットには誤りを検出するためのデータが埋め込まれています。
誤り検出は、買い物のときに使うバーコードや書籍のISBN(国際標準図書番号)のバーコード、クレジットカードの16桁の番号などでも使われています。これらの数字が誤って入力またはスキャンされた場合には、誤り検出がi働いてデータの再入力を要求します。
この章を読み終えるまでに、誤り制御符号の基本的な考え方を学ぶことができるでしょう。必要な理由、誤り検出と誤り訂正のアルゴリズムの違い、(手品で見た)パリティとチェックディジットが本の番号、バーコード、クレジットカード番号で使われている具体例です。
9.2. The Parity Magic Trick
If you have never seen the parity magic trick before, check out the video in the “What’s the Bigger Picture?” section above. This section assumes that you know what is meant by the parity magic trick, but now we’ll explain how it actually works!
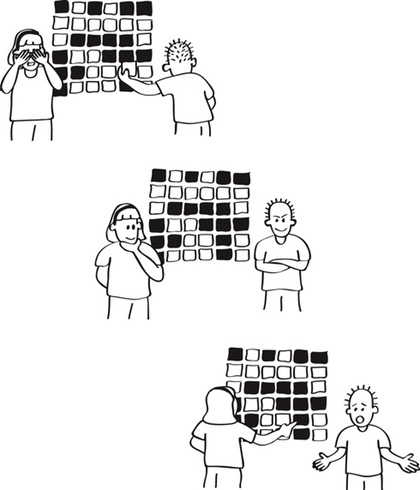
A magician asks an observer to lay out a square grid of two-sided cards, and the magician then says they are going to make it a bit harder, and add an extra row and column to the square. The magician then faces the other way while the observer flips over one card. The magician turns back around again, and tells the observer which card was flipped!
The question now is, how did the magician know which card had been flipped without seeing the card being flipped, or memorising the layout?! The short answer is error control coding. Let’s look more closely at that…
9.2.1. Carrying out the parity trick
You are now going to take the role of the magician and carry out the trick yourself. The interactive below will allow you to practice it.
In the interactive, the computer has a 7x7 grid of black and white cards. You must choose the colour of an extra card for each row (at the right) and column (at the bottom), making an 8x8 grid of cards. Each extra card should be chosen so that each row and column has an even number of black cards (since there are 8 cards, there will also be an even number of white cards). The bottom right-hand card can be chosen from either its row or column; they should both give the same colour. Once you think you have this correct, you should tell the computer to flip a card. An animation will appear for a few seconds, and then the cards will reappear with one card flipped (all the rest will be the same as before). Your task is to identify the flipped card. You should be able to do this without having memorised the layout. Remember the pattern you made with the extra cards you added? That’s the key to figuring it out. Once you think you have identified the card, click it to see whether or not you were right! The interactive will guide you through these instructions. If you are completely stuck identifying the flipped card, a hint follows the interactive, although you should try and figure it out for yourself first! Make sure you add the extra cards correctly; the computer won’t tell you if you get them wrong, and you probably won’t be able to identify the flipped card if the extra cards aren’t chosen correctly.
★コンテンツは準備中です★
Remember how you made it so that each column had an even number of black cards? When a card is flipped, this results in the row and column that the card was in having an odd number of black cards. So all you need to do is to identify the row and column that have an odd number of black and white cards, and the card that is at the intersection of them must be the one that was flipped!
9.2.2. How does this relate to computer science?
What we saw above is a simple error control coding algorithm, known as 2-dimensional parity.
The cards represent bits, with their two states being black and white (in the “data representation” chapter we looked at how a bit can be stored by anything that can be in one of two states: shiny/not shiny, magnetised/not magnetised, high voltage/low voltage, black/white, etc). The original 7x7 cards that the computer laid out for you could be some kind of data, for example some text represented using bits, or an image, or some numbers. Although they are laid out in a grid, on a computer the rows of bits would be stored or transmitted one after the other (as 8 lots of 8 bits).
The extra cards you added are called parity bits. Parity simply means whether a number is even or odd (the word comes from the same root as “pair”). By adding the extra cards in a way that ensured an even number of black cards in each row and column, you made it so that the rows and columns had what is called even parity.
When a card was flipped, this simulated an error being made in your data (such as a piece of dust landing on a bit stored on a CD, or a cosmic ray changing a bit stored on a hard disk, or electrical interference changing a bit being sent over a network cable). Because you knew that each row and column was supposed to have an even number of black and white cards in it, you could tell that there was an error from the fact that there was a column and row that had an odd number of black cards in it. This means that the algorithm is able to detect errors, i.e. it has error detection. The specific card that had been flipped was at the intersection of the row and column that had an odd number of black cards and white cards in them, and because you were able to identify exactly which card was flipped, you were able to correct the error, i.e the algorithm has error correction.
If you had not added the parity bits, you would have had no way of even knowing an error had occurred, unless you had memorised the entire layout of cards! And what if more than one bit had been flipped? We’ll consider this later.
Project:
Being a magician
Now that you have learnt how the parity trick works, you might like to try it with a physical set of cards like the busker in the video, or you could use any objects with two distinct sides, such as coins or cups. You could use playing cards, but the markings can be distracting, and cards with two colours are easiest (you can make them by cutting up sheets of card with the two colours on, or single coloured card with a scribble or sticker on one side).
You can find details and lots of ideas relating to the trick here, or follow these instructions:
- Ask a friend to lay out 25 cards in a 5 by 5 grid, trying to have a reasonably random mix of blacks and whites (this is smaller than the one in the interactive, but it is easier to have fewer cards to avoid errors in the next step!)
- Take all the remaining cards, and then say that actually, 5 by 5 is too easy so you are going to make it 6 by 6. Instead of adding the new row and column randomly though, you are adding them in the way you did in the interactive (even parity). Do this as fast as you can without making errors (it can look very casual if you practise this, even though the cards are being carefully selected).
- Tell your friend that you are going to face the other way, and you want them to flip over one card while you are not looking.Check that they’ve flipped exactly one card.
- Turn around again once they have flipped a card, look through the rows and columns, identifying a row and then a column that has an odd number of black cards in it. The flipped card will be the one at the intersection of that row and column. Flip that card back over.
It would take some practice to be able to add the extra cards, and identify the flipped card without the observer noticing that you are thinking hard about it. With practice you should be able to do it while having a casual conversation. Once you master it, you’ve got a great trick for parties, or even for busking.
To make it more showy, you can pretend that you are mind reading the person, waving your hands over the cards. A particular impressive variation is to have an assistant come in to the room after the card has been flipped; even though they haven’t seen any of the setup, they will still be able to detect the error.
9.2.3. Investigating the parity trick a little further
At this point, you should be able to carry out the parity trick well enough that you can demonstrate that you understand how to do it. The remainder of this section is focussed on exploring further ideas in error control coding related to the parity trick. You can either continue to read through the rest of this section and explore the interesting questions raised, or you can skip forward to one of the other sections.
It would be ideal to have some physical parity cards at this point that you can layout in front of you and play around with to explore the questions raised.
An error control coding algorithm can often detect errors more easily than it can correct them. Errors involving multiple bits can sometimes even go undetected. What if the computer (or your friend if you were being a magician with actual parity cards) had been sneaky and turned over two cards instead of one? You could start by getting a friend or classmate to actually do this. Repeat it a few times. Are you always able to correct the errors, or do you get it wrong?
Remember that to detect errors using this algorithm, you know that if one or more rows and/or columns has an odd number of blacks and whites in it, that there must be at least one error. In order to correct errors you have to be able to pinpoint the specific card(s) that were flipped.
Are you always able to detect when an error has occurred if 2 cards have been flipped? Why? Are you ever able to correct the error? What about with 3 cards?
There is actually a way to flip 4 cards where the error is then undetected meaning that the algorithm will be unable to detect the error. Can you find a way of doing this?
With more parity cards, we can detect and possibly correct more errors. Lets explore a very simple system with minimal parity cards. We can have a 7x7 grid of data with just one parity card. That parity card makes it so that there is an even number of black cards in the entire layout (including the parity card). How can you use this to detect errors? Are you ever able to correct errors in this system? In what situations do errors go undetected (think when you have multiple errors, i.e. more than one card flipped).
So going back to the actual parity trick that has the 7 by 7 grid, and 15 parity cards to make it 8 by 8, it is interesting to note that only 1 extra card was needed to detect that an error had occurred, but an extra 15 cards were needed to be able to correct the error. In terms of the cost of an algorithm, it costs a lot more space to be able to correct errors than it does to be able to simply detect them!
What happens when you use grids of different sizes? The grid doesn’t have to have an even number of black cards and an even number of white cards, it just happens that whenever you have an even number sized grid with the parity bits added (e.g. the 8x8 we have mostly used in this section) and you have an even number of black cards, you will also have to have an even number of whites, which makes it a bit easier to keep track of.
Try a 6x6 grid with parity cards to make it 7x7. The parity cards simply need to make each row and column have an even number of black cards (in this case there will always be an odd number of white cards in each row and column). The error detection is then looking for rows and columns that have an odd number of black cards in them (but an even number of white cards). Interestingly, the grid doesn’t even have to be a square! You could use 4x7 and it would work!
There’s also no limit on the size. You could create a 10x10 grid (100 cards), and still be able to detect which card has been flipped over. Larger grids make for an even more impressive magic trick.
9.3. Check digits on barcodes and other numbers
You probably wouldn’t be very happy if you bought a book online by entering the ISBN (International Standard Book Number), and the wrong book was sent to you, or if a few days after you ordered it, you got an email saying that the credit card number you entered was not yours, but was instead one that was one digit different and another credit card holder had complained about a false charge. Or if you went to the shop to buy a can of drink and the scanner read it as being a more expensive product. Sometimes, the scanner won’t even read the barcode at all, and the checkout operator has to manually enter the number into the computer — but if they don’t enter it exactly as it is on the barcode you could end up being charged for the wrong product. These are all examples of situations that error control coding can help prevent.
Barcode numbers, credit card numbers, ISBNs, the NHI (National Health Index, the unique identifier given to all users of the NZ health system), IRD numbers (Inland Revenue Department number for all NZ taxpayers) all have error control coding in them to help reduce the chance of errors. The last digit in each of these numbers is a check digit, which is obtained doing a special calculation on all the other digits in the number. If for example you enter your credit card number into a web form to buy something, it will calculate what the 16th digit should be, using the first 15 digits and the special calculation (there are 16 digits in a credit card number). If the 16th digit that it expected is not the one you entered, it can tell that there was an error made when the number was entered and will notify you that the credit card number is not valid.
In this section we will be initially looking at one of the most commonly used barcode number formats used on most products you buy from supermarkets and other shops. We will then be having a quick look at credit card numbers. You don’t have to understand why the calculations work so well (this is advanced math, and isn’t important for understanding the overall ideas), and while it is good for you to know what the calculation is, it is not essential. So if math is challenging and worrying for you, don’t panic too much because what we are looking at in this section isn’t near as difficult as it might initially appear!
The end of this section contains a subsection on how you could use this material for an assessed report (based on New Zealand NZQA AS2.44)
9.3.1. Check Digits On Product Barcodes
Most products you can buy at the shop have a barcode on them with a 13 digit global trade item number (referred to as GTIN-13). The first 12 digits are the actual identification number for the product, the 13th is the check digit calculated from the other 12. Not all barcodes are GTIN-13, there are several others around. If the barcode has 13 numbers in it, it is almost certainly GTIN-13.
The following interactive checks GTIN-13 barcodes. Enter the first 12 numbers of a barcode (correctly!) into the interactive, and it will say what it expects the 13th digit to be. Start by using the barcode number of a box of 30 cans of coke; “9 300675 036009”. Check that it correctly calculates the last digit is 9 after you put in the first 12.

Have a look for another product that has a barcode on it, such as a food item from your lunch, or a stationery item. Your teacher might also bring various packaging that has barcodes on it for you to try. Note that some barcodes are a little different. Make sure the barcodes that you are using have 13 digits (although you might like to go and find out how the check digit works on some of the other ones). Hopefully you will find that the interactive is always able to determine the check digit correctly!
Try changing one of the digits in a barcode number. What happens with the check digit? This is the key to error detection — if a number is typed in incorrectly, the check digit probably won’t match. For example, one of the following product numbers has one digit incorrect. Can you tell which of the products is wrong?
- 9 400550 619775
- 9 400559 001014
- 9 300617 013199
If you were scanning the above barcodes in a supermarket, the incorrect one will need to be rescanned, and the system can tell that it’s a wrong number without even having to look it up.
You could try swapping barcode numbers with a classmate, but before giving them the number toss a coin, and if it’s heads, change one digit of the barcode before you give it to them. Can they determine that they’ve been given an erroneous barcode?
So, what is the calculation used to get the check digit? You might have noticed the button on the interactive that says “Show calculations”. This shows how the check digit was calculated. It’s a simple calculation: each for the first 12 digits is multiplied by either 1 or 3 (the first digit is multiplied by 1, the second by 3, the third by 1, and so on), and these values are added up. For example, for the barcode 9 400559 001014 the sum is (9 x 1) + (4 x 3) + (0 x 1) + (0 x 3) + (5 x 1) + (5 x 3) +(9 x 1) + (0 x 3) + (0 x 1) + (1 x 3) + (0 x 1) + (1 x 3), which adds up to 56. You then subtract the sum from nearest equal or higher multiple of ten. The next multiple of 10 after 56 is 60, and 60-56 is 4, so the checksum should be 4.
If one of the digits is incorrect, this calculation will produce a different value to the checksum, and signals an error. So single digit errors will always be detected, but what if two digits change — will that always detect the error?
What if the error is in the checksum itself but not in the other digits - will that be detected?
9.3.2. How do check digits protect against common human errors?
People can make mistakes when they enter numbers into computers, and even barcode scanners can get a digit wrong. Check digits attempt to detect when an error has occurred and notify the computer and/or person of it. Suppose you give your cellphone number to a friend so that they can contact you later. To ensure that you told them the number correctly, you may get them to text you immediately to confirm (and so that you have their number too). If you don’t get the text you will probably double check the number and will find that your friend made an error, for example they got a digit wrong or they reversed 2 digits next to one another. Mistakes happen, and good systems prevent those mistakes from having annoying or even serious consequences. If a check digit is being used, there is a good chance that the error will be detected when the check digit is not what the computer expects it to be.
Some of the really common errors are:
Getting one digit wrong (substitution)
Swapping two digits that are adjacent (transposition)
Missing a digit
Adding a digit
The last two will be picked up from the expected length of the number; for example,a GTIN-13 has 13 digits, so if 12 or 14 were entered, the computer immediately knows this is not right. The first two depend on the check digit in order to be detected. Interestingly, all one digit errors will be detected by common checksum systems, and most transpositions will be detected (can you find examples of transpositions that aren’t detected, using the interactive above?)
There are also some less common errors that people make
Getting a digit wrong in two or more different places
Doubling the wrong digit, e.g. putting 3481120 instead of 3481220
Muddling 3 digits, e.g. 14829 instead of 12489
Phonetic errors are possible when the number was read and typed by somebody listening (or reading the number to themselves as they type it). For example, "three-forty" (340) might be heard as "three-fourteen" (314), and numbers like 5 and 9 can sound similar on a bad phone line.
Experiment further with the interactive. What errors are picked up? What errors can you find that are not? Are the really common errors nearly always picked up? Can you find any situations that they are not? Try to find examples of errors that are detected and errors that are not for as many of the different types of errors as you can.
9.3.3. How is the check digit on product barcodes calculated?
The first 12 digits of the barcode represent information such as the country origin, manufacturer, and an identifier for the product. The 13th digit is a check digit, it is calculated from the first 12 digits. It is calculated using the following algorithm (also, see the example below).
- Multiply every second digit (starting with the second digit) by 3, and every other digit by 1 (so they stay the same).
- Add up all the multiplied numbers to obtain the sum.
- The check digit is whatever number would have to be added to the sum in order to bring it up to a multiple of 10 (i.e. the last digit of the sum should be 0). Or more formally, take the last digit of the sum and if it is 0, the check digit is 0. Otherwise, subtract the last digit from 10 to obtain the check digit.
Lets look at an example to illustrate this algorithm. We want to confirm that the check digit that was put on the barcode of a bottle of coke was the correct one. Its barcode number is 9300675032247. The last digit, 7, is the check digit. So we take the first 12 digits and multiply them by 1 or 3, depending on their positions (9x1+3x3+0x1+0x3+6x1+7x3+5x1+0x3+3x1+2x3+2x1+4x3). We then add up all the multiplied numbers, obtaining a sum of 73. We want to add the check digit that will bring the sum up to the nearest multiple of 10, which is 80. This number is 7, which is indeed the check digit on the coke bottle’s barcode.
The following interactive can be used to do the calculations for you. To make sure you understand the process, you need to do some of the steps yourself; this interactive can be used for a wide range of check digit systems. To check a GTIN-13 number, enter the first 12 digits where it says "Enter the number here". The multipliers for GTIN-13 can be entered as "131313131313" (each alternating digit multiplied by 3). This will give you the products of each of the 12 digits being multiplied by the corresponding number. You should calculate the total of the products (the numbers in the boxes) yourself and type it in. Then get the remainder when divided by 10. To work out the checksum, you should calculate the digit needed to make this number up to 10 (for example, if the remainder is 8, the check digit is 2). If the remainder is 0, then the check digit is also 0.
Try this with some other bar codes. Now observe what happens to the calculation when a digit is changed, or two are swapped.
The algorithm to check whether or not a barcode number was correctly entered is very similar. You could just calculate the check digit and compare it with the 13th digit, but a simpler way is to enter all 13 digits.
Multiply every second digit (starting with the second digit) by 3, and every other digit by 1. This includes the 13th digit, which is multiplied by 1. Add up all the multiplied numbers to obtain the total. If the last digit of the sum is a 0, the number was entered correctly. (That's the same as the remainder when divided by 10 being 0).
Curiosity: Working out a checksum in your head
For 13-digit barcodes, a quick way to add up a checksum that can be done in your head (with some practice) is to separate the numbers to be multiplied by 3, add them up, and then multiply by 3. For the example above (9300675032247) the two groups are 9+0+6+5+3+2+7 = 32 and 3+0+7+0+2+4= 16. So we add 32 + 16x3, which gives the total of 80 including the check digit.
To make it even easier, for each of the additions you only need to note the last digit, as the other digits will never affect the final result. For example, the first addition above begins with 9+0+6, so you can say that it adds up to 5 (rather than 15) and still get the same result. The next digit (5) takes the sum to 0, and so on. This also means that you can group digits that add to 10 (like 1 and 9, or 5 and 5), and ignore them. For exam ple, in the second group, 3+0+7 at the start adds up to 0, and the only sum that counts is 2+4, giving 6 as the total.
Finally, even the multiplication will be ok if you just take the last digit. In the example above, that means we end up working out 6x3 giving 8 (not 18); the original was 16x3 giving 48, but it's only the final 8 digit that matters.
All these shortcuts can make it very easy to track the sum in your head.
Extra For Experts: Why does this algorithm work so well?
In order to be effective, the algorithm needs to ensure the multiplied digits will not add up to a multiple of 10 any more if the digits are changed slightly. The choice of multipliers affects how likely it is to detect small changes in the input. It's possible to analyse these mathematically to work out what sorts of errors can be detected.
The check digit on barcodes is described in the chapter on error control coding. Basically every second digit is multiplied by 3, and the sum of these multiples are added to the remaining digits.
Lets look at some smaller examples with 5 digits (4 normal digits and a check digit), as the same ideas will apply to the 13 digit numbers.
If we need a check digit for 8954, we would calculate (8x1)+(9x3)+(5x1)+(4x3)=52, and in order to bring this up to 60, we need to add 8. This makes the full number 89548.
The first thing we should observe is that only the ones column (last digit) of each number added have any impact on the check digit. 8+27+5+12=52, and 8+7+5+2=22 (only looking at the last digit of each number we are adding). Both these end in a 2, and therefore need 8 to bring them up to the nearest multiple of 10. You might be able to see why this is if you consider that the “2” and “1” were cut from the tens column, they are equal to 10+20=30, a multiple of 10. Subtracting them only affects the tens column and beyond. This is always the case, and therefore we can simplify the problem by only adding the ones column of each number to the sum. (This can also be used as a shortcut to calculate the checksum in your head).
Protection against single digit errors
Next, lets look at why changing one digit in the number to another digit will always be detected with this algorithm. Each digit will contribute a number between 0 and 9 to the sum (remember we only care about the ones column now). As long as changing the digit will result in it contributing a different amount to the sum, it becomes impossible for it to still sum to a multiple of 10. Remember that each digit is either multiplied by 1 or 3 before its ones column is added to the sum.
A number being multiplied by 1 will always contribute itself to the sum. If for example the digit was supposed to be 9, no other single digit can contribute 9 to the sum. So those multiplied by 1 are fine.
But what about those multiplied by 3? To answer that, we need to look at what each different digit contributes to the sum when multiplied by 3.
1 -> 3
2 -> 6
3 -> 9
4 -> 2 (from 12)
5 -> 5 (from 15)
6 -> 8 (from 18)
7 -> 1 (from 21)
8 -> 4 (from 24)
9 -> 7 (from 27)
0 -> 0
If you look at the right hand column, you should see that no number is repeated twice. This means that no digit contributes the same amount to the sum when it is multiplied by 3!
Therefore, we know that all single digit errors will be detected.
Protection against swapping adjacent digit errors
Seeing why the algorithm is able to protect against most swap errors is much more challenging.
If two digits are next to one another, one of them must be multiplied by 1, and the other by 3. If they are swapped, then this is reversed. For example, if the number 89548 from earlier is changed to 85948, then (5x3)+(9x1)=24 is being added to the total instead of (9x3)+(5x1)=32. Because 24 and 32 have different values in their ones columns, the amount contributed to the total is different, and therefore the error will be detected.
But are there any cases where the totals will have the same values in their ones columns? Another way of looking at the problem is to take a pair of rows from the table above, for example:
8 -> 4
2 -> 6
Remember that the first column is how much will be contributed to the total for digits being multiplied by 1, and the second column is for those being multiplied by 3. Because adjacent digits are each multiplied by a different amount (one by 3 and the other by 1), the numbers diagonal to each other in the chosen pair will be added.
If for example the first 2 digits in a number are “28”, then we will add 2+4=6 to the sum. If they are then reversed, we will add 8+6=14, which is equivalent to 4 as again, the “10” part does not affect the sum. 8+6 and 2+4 are the diagonals of the pair!
8 -> 4
2 -> 6
So the question now is, can you see any pairs where the diagonals would add up to the same value? There is one!
Protection against twin errors
A twin error is where a digit that is repeated twice in a number is changed to a different digit that is repeated twice. For example, if we have “22” in the number, somebody might somehow change it to “88”.
When two numbers are side by side, one is multiplied by 3 and the other by 1. So the amount contributed to the total is the sum of the number’s row in the above table. For example, 2 has the row “2->6”. This means that 2+6=8 will be contributed to the sum as a result of these two digits.
If any rows add up to the same number, this could be a problem. Where the sum was over 10, the tens column has been removed.
1 -> 3 adds to “4”
2 -> 6 adds to “8”
3 -> 9 adds to “2”
4 -> 2 adds to “6”
5 -> 5 adds to “0”
6 -> 8 adds to “4”
7 -> 1 adds to “8”
8 -> 4 adds to “2”
9 -> 7 adds to “6”
0 -> 0 adds to “0”
Some of the rows add up to the same number! Because both 4 and 9 add up to 6, the error will not be detected if “44” changes to “99” in a number!
Rows that do not add will be detected. From the example above, if 22 changes to 88, this will be detected because 22’s total is 8, and 88’s total is 2.
An error that is never detected
Another error that people sometimes make is the jump transposition error. This is where two digits that have one digit in between them are swapped, for example, 812 to 218.
A pair of numbers that are two apart like this will always be multiplied by the same amount as each other, either 1 or 3. This means that the change in position of the numbers does not affect what they are multiplied by, and therefore what they contribute to the sum. So this kind of error will never be detected.
Project: Project with check sums
The following interactive will generate random numbers of a chosen type (e.g. ISBN numbers for books). These numbers are random, and are not based on numbers for actual books (or bank accounts!) This means that you can do this project without having to ask people for their personal information such as credit card numbers (in fact, they shouldn't give you this information anyway!)
Although the numbers from this interactive are random, their check digits are calculated using the appropriate method, so you can use them as examples for your project. Actually, not all of them will be correct, so one of your challenges is to figure out which are ok!
Your project is to choose a checksum other than the 13-digit barcodes, and research how it is calculated (they all use slightly different multipliers). You should demonstrate how they work (using the following interactive if you want), and find out which of the numbers generated are incorrect.
ISBN-10 is particularly effective, and you could also look into why that is.
9.3.4. The whole story!
The codes discussed in this chapter are all widely used, but the most widely used codes for data storage are more sophisticated because they need to deal with more complex errors than a single bit changing. For example, if a CD is scratched of a hard disk has a small fault, it’s likely to affect many adjacent bits. These systems use codes based on more advanced mathematical concepts. The most widely used codes for storage and data transfer are the Reed-Solomon codes and Cyclic Redundancy Check (CRC). For human readable numbers such as bar codes, bank numbers, tax numbers, social security numbers and so on, checksums are very common, and the Luhn algorithm is one of the more widely used. Larger checksums are also used to check that downloaded files are correct. The parity method is a form of Hamming code.
9.4. Further reading
9.4.1. Useful Links
- CS Unplugged Parity Trick
- CS4FN has a free book that contains the Parity Trick and a number of other tricks related to computer science.
- Techradar has more information about error detection and correction
- An explanation of error correcting codes
- A check digit calculator for common bar codes
Computer Science Field Guide is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 3.0 Unported License.
Produced by Tim Bell, Jack Morgan, and many others based at the University of Canterbury, New Zealand.